
Update March, 2023:
New Working Paper from JK Dagsvik :Equilibria in Logit Models of Social Interaction and Quantal Response Equilibrium
Update March, 2021:
New paper from Irecohex in Journal of Choice Modelling
The paper "Predicting strategic medical choices: An application of a quantal response equilibrium choice model" by Ge and Godager is now in press in Journal of Choice Modelling. A a quantal response equilibrium choice (QREC) model is applied in analyzing multi-criteria games where subjects have altruistic (patient-regarding) preferences. A consistent and robust two-step maximum likelihood estimator can easily be acquired by means of ready-made software for estimating generalized multinomial logit models.
In order to to assess the usefulness of the QRE assumption in predicting human behavior when the λ parameter is unknown ex-ante, Ge and Godager predict strategic choices out-of-sample.
Their paper introduce important nuance to the recent literature on how competition influences human behavior. The results show that even with fixed pro-social preferences, the behavioral response to competition in a laboratory experiment can be substantial.
YouTube channel
Example
An example of a game with a unique QRE is given in (a). An example of a game with a unique logit QRE for λ<0.67 and 3 logit QRE λ>0.68 is given in (b):
a)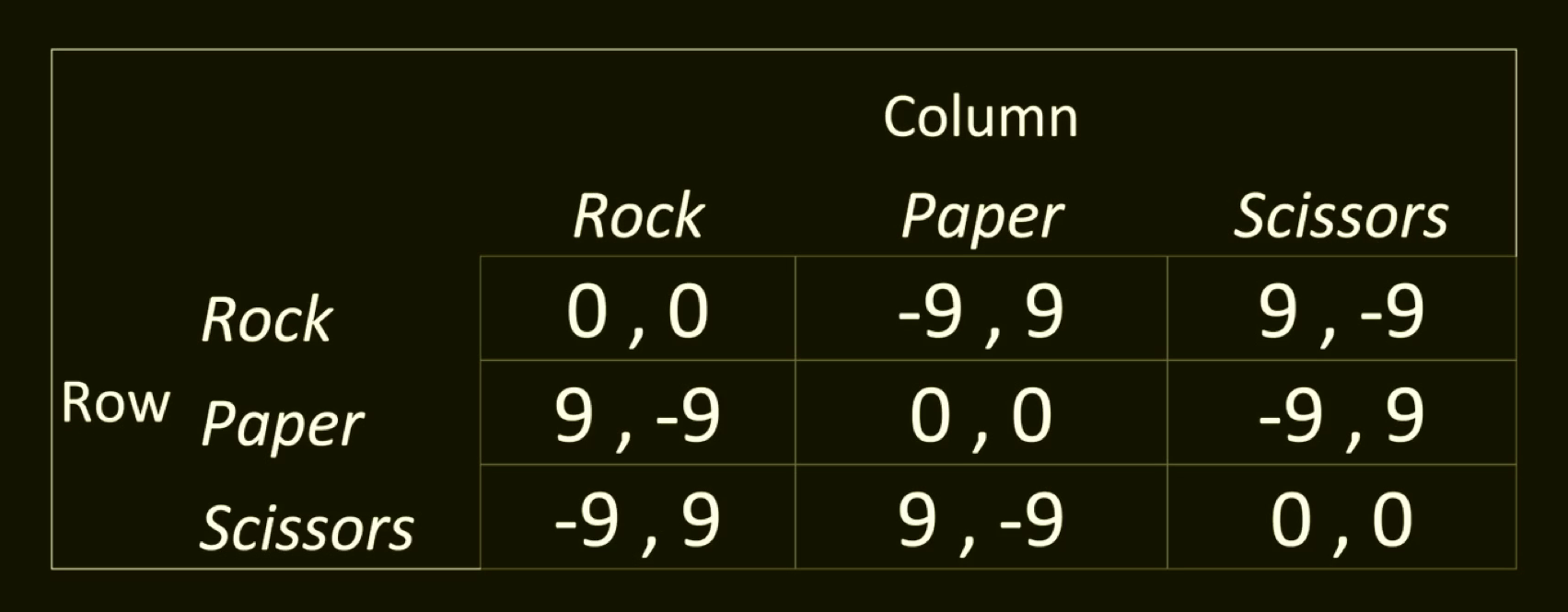 b)
b)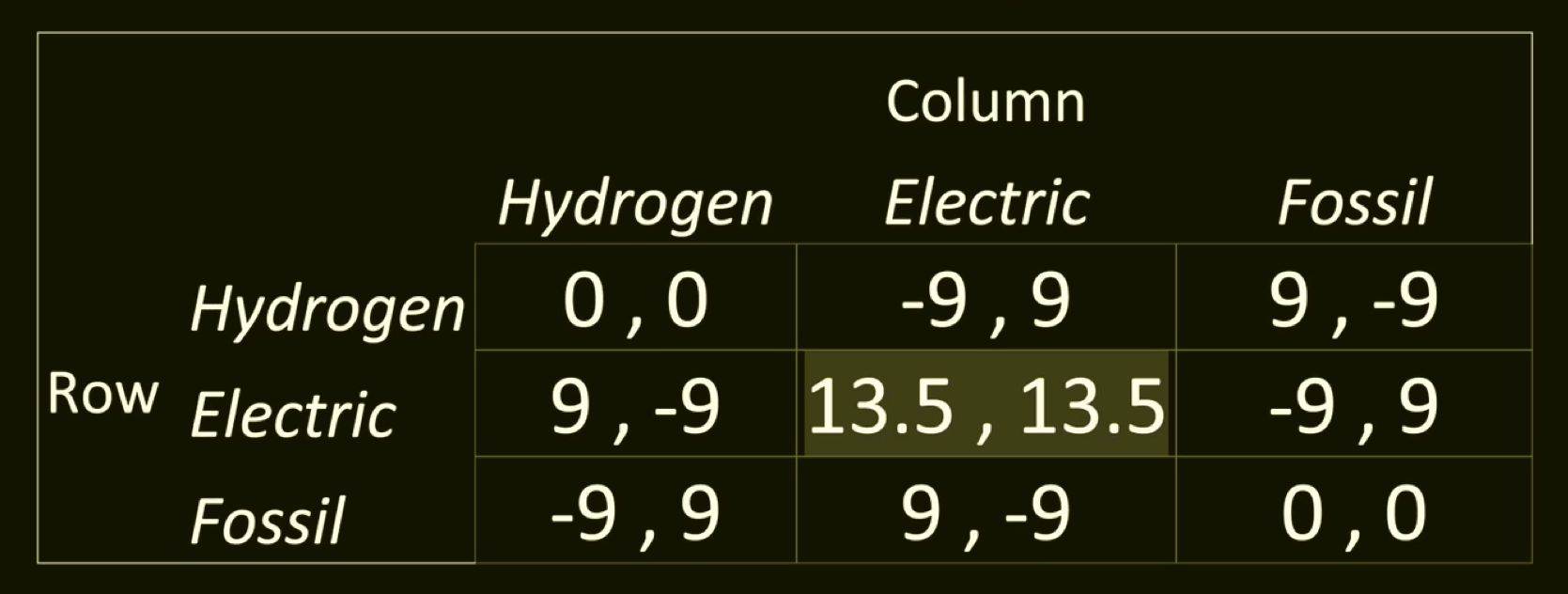
Equilibrium correspondence for game b) is plotted in the probability simplex c) (0<λ ≤0.60) , d) (0<λ ≤0.70) and e) (0<λ ≤19.70) :
c)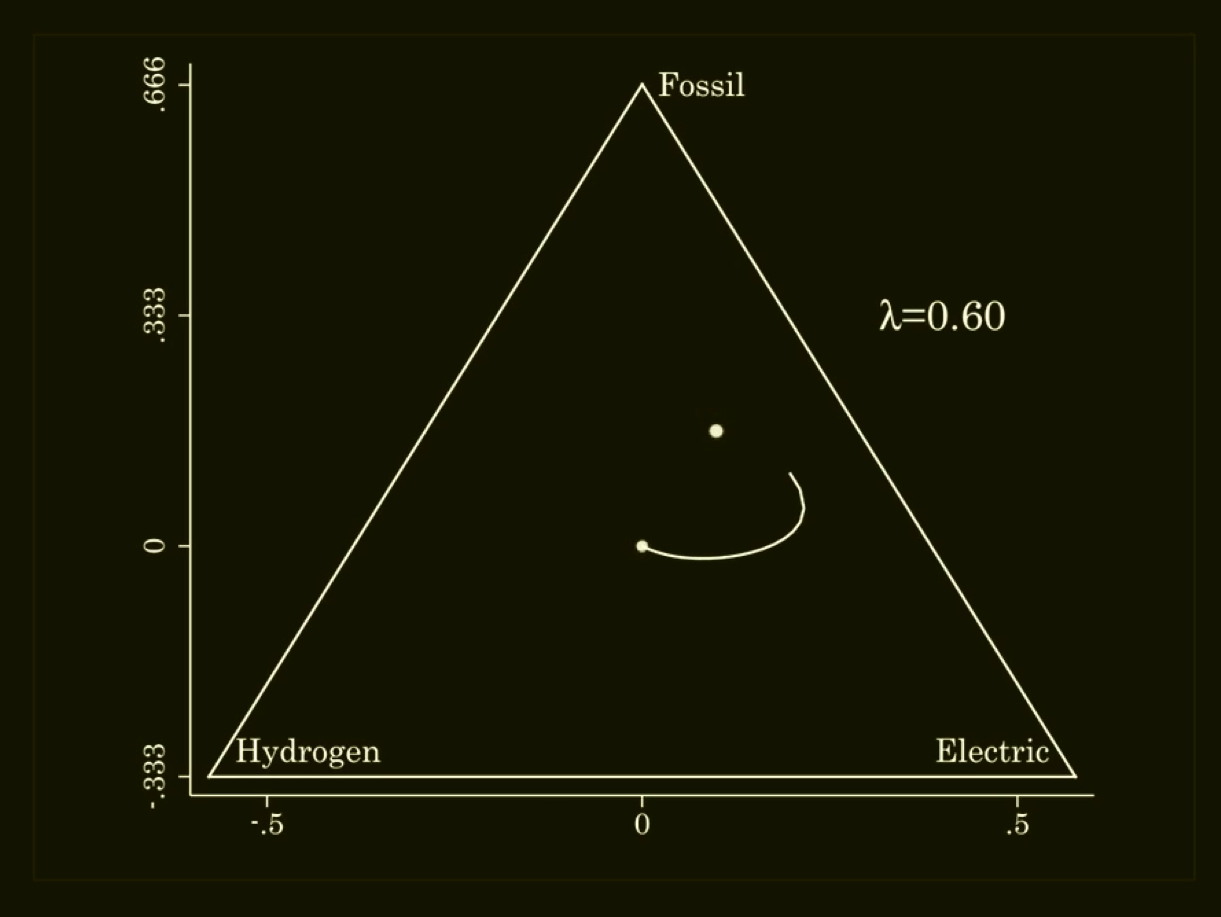 d)
d)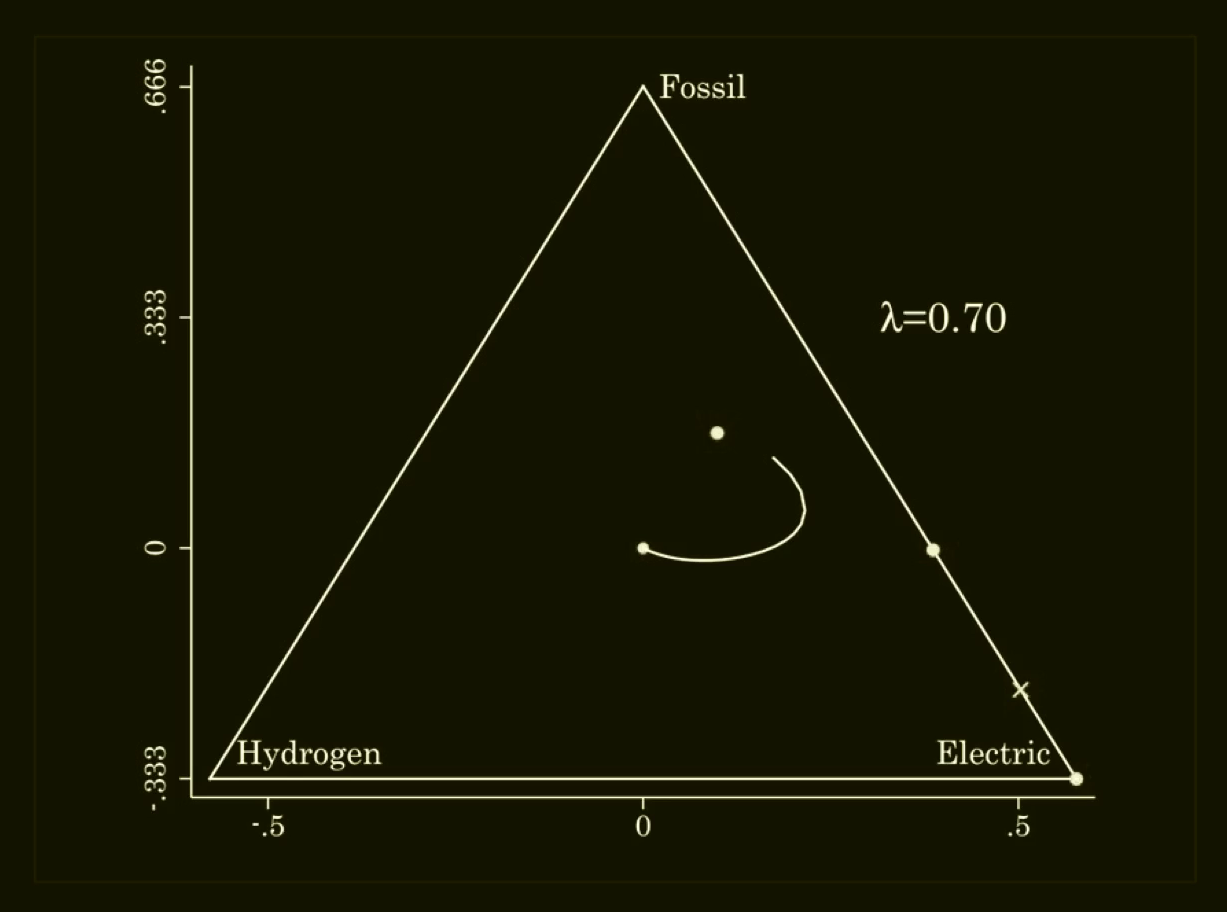 e)
e)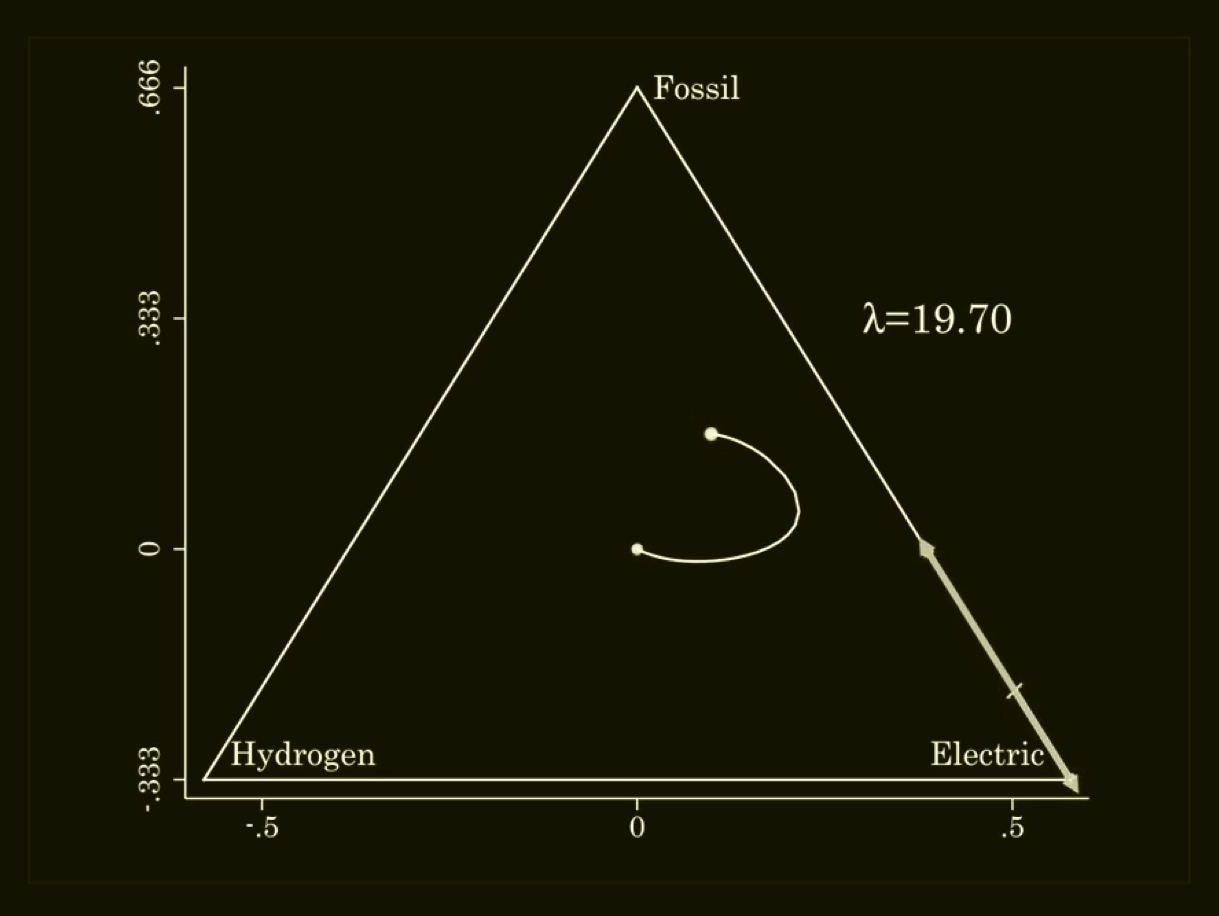
In d), we see how two additonal QREs that were absent for λ=0.60 have appeared for λ=0.70. The additional two QRE are located along the edge of the probability simplex where the probability of the pure strategy "Hydrogen" is zero. Interestingly, these two equilibria can be hard to find. They are not found by Gambit.
The reason that Gambit and similar software does not provide these additional equilibria, is that the programs compute the equilibrium correspondence starting in the unique equilibrium in the centroid.
The QRE with a high probability of playing "Electric" in game b) above has much intuitive appeal, and still remain undetected by Gambit and similar software. However, from the theorems of John K. Dagsvik (2020), it is easy to show that the game has three QRE whenever λ>0.68. When it is known that a game has multiple QRE, one can initiate a broader search for equilibria which are not located on the branch starting in the centroid. Data and STATA commands for reproducing this particular example with 3 QRE can be downloaded here. Excel file with coordinates and equilibrium points can be downloaded here.
Update October 6, 2020:
Games may have multiple quantal response equilibria (QRE).
In the working paper by John K. Dagsvik, criteria are established that characterize the set of logistic-QRE. Necessary and sufficient conditions for uniquenes are provided. The provided algorithms are useful for establishing how many equilibria that exist in the case of multiple equilibria.
The paper can be downloaded here
Contact:
Geir Godager, Department of Health Management and Health Economics, University of Oslo
Email: geir.godager(at)medisin.uio.no